A Physical Therapist's Guide to Logic-and-Bayes-informed Clinical Reasoning

A prerequisite for Evidence-informed practice

What started as a sketch to organize my thoughts in preparation for a discussion with my friend and colleague

Timothy Duffy

, turned into more of a cheatsheet that could be used for physical therapy students during their didactic or clinical studies, a practicing physical therapist, or anyone else really since the fields of logic and mathematics are definitely not constrained to the physical therapy field. In fact, they are rarely spoken of outside of physical therapy academic circles. I hope to help change that.

Statistics, logic, and clinical inquiry I would contend, are usually of minor focus in the minds of physical therapy students due to the high demands of their endeavors to learn clinical anatomy, neuroanatomy, pathology, musculoskeletal, and other areas of studies that are easily considered highly relevant in the edification of a future physical therapist. It may be because they are generally a minor part of a program’s curriculum, save for the research project component, and might be included within other topics as an aside . An exception to the rule was Plymouth State University, where their mission included the acknowledgment of the gap between epistemology and ontology and the development of knowledge, however this effort was recently and unfortunately extinguished.

I think a part of lack of emphasis on clinical inquiry comes from the lack of exposure to logic and inferencing, minimal reflection on our own concepts of causation, and generally unchallenged heuristical and traditional modes of thinking.

Even for those interested and energized by these discussions, the mathematics and overly complex presentation of logical thinking can make the process feel daunting and hopeless.

My brain is happiest when new concepts are connected to other known models, much like the concept of syntopical reading. I don’t know how else one makes sense of new information without comparing it to something one already knows. It’s the relative nature of our epistemological way of perching the world, I suppose. I digress, the point is that information needs to be connected. If you have lots of new information that is somehow connected, seeing a model of their connectedness can be helpful.

At first, try not to be overwhelmed. Take comfort that if you are reading this, you may have some part of the understanding already, so if you can latch onto any part presented in the model, you are only a small step away from making the leap to understanding the adjacent parts, then the model as a whole. Or better, have faith that the model logically connects the parts and use it to bridge your present understanding to the parts unknown to you.

Without further ado, I give you my first draft of the cheatsheet: This will be subject to revisions, corrections, etc as I continue my journey into discovering, knowing, and presenting.

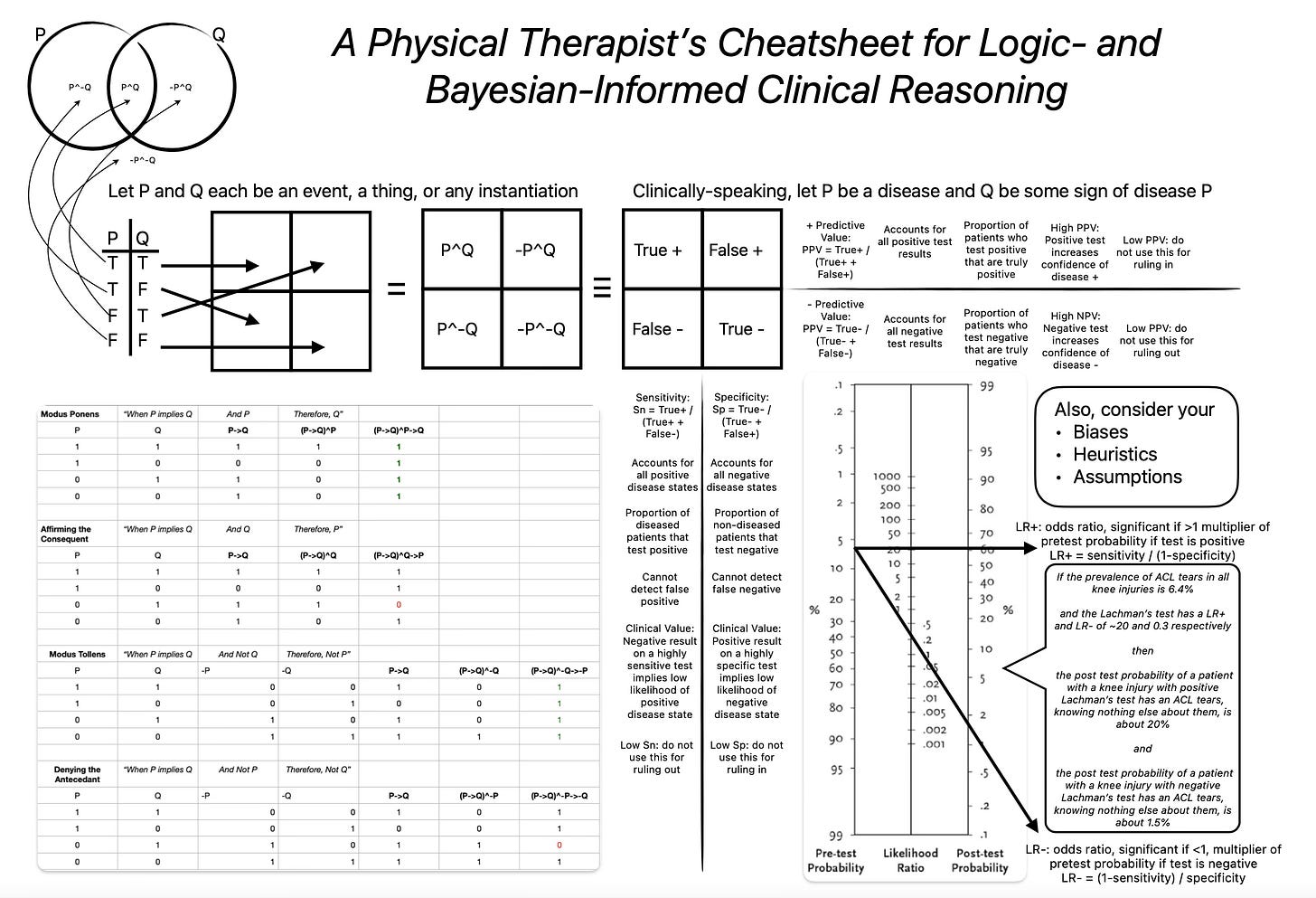
The image shows a Venn diagram of two expressions P, Q. Sometimes they occur alone, sometimes together, and sometimes not at all.

I introduce a basic truth table showing the possible states of P,Q. The rows translate into a 2x2 grid, and I fill in the states of the expressions.

This is equivalent to a 2x2 for disease and test states. This is the connection of P being a disease and Q being a test. They can each be true or false.

• The number of true positives (top left quadrant) and false negatives (bottom left quadrant) are used to calculate sensitivity (True+ / (True+ + False-)

• The number of true negatives (bottom right quadrant) and false positives (top right quadrant) are used to calculate specificity (True- / (True- + False+)

• The number of true positives and false negatives are used to calculate positive predictive value (True+ / (True+ + False +)

• The number of true positives and false negatives are used to calculate negative predictive value (True- / (True- + False -)

• Likelihood ratios (LR) are calculated using sensitivity and specificity values. These are odds ratios which modify your pre-test probability (which may be informed by disease prevalence or your hypothesis based patient interview and observation). LR+ is the multiplier used if your test for the disease is positive. Likewise, LR- is the multiplier used if your test for the disease is negative.

  • Your pre-test probability gets marked on the left hand line of the Bayesian nomogram, the LR+

  • Your LR+ (if test is positive) or LR- (if test is negative) gets marked on the center line

  • You literally draw a straight line connecting your pretest probability and odds ratio (multiplier) and continue it until it bisects the right-hand line which is your new probability for the disease being present.

I provide a note to self to challenge your thinking. You may have your own assumptions or biases about the patient, disease prevalence, MOI, own clinical skills, or otherwise that may affect your ability to attain accurate pretest probability, administer a test, or interpret the results that may affect your opinion. You may see a lot of disease X and be more prone to believe that the next case similar to these could be disease X (availability heuristic). It is useful to be aware of these potential sources of erroneous clinical reasoning.

Finally, I included a truth table of some common conditional statements. This can be a quick check for your gut response to new information or for interpreting other peoples reasoning. Please, do not weaponize this new tool! Note: a tautology means that a statement is true in all states (each row of expression states)

Modus Ponens: If P implies Q, and P is true, then Q is true (VALID, tautology).

Clinical example: If an ACL tear implies a positive Lachman’s test, and the patient has an ACL tear, that patient will have a positive Lachman’s test

Modus Tollens: If P implies Q, and Q is false, then P is false (VALID, tautology)

Clinical example: If an ACL tear implies a positive Lachman’s test, and the patient has a negative Lachman’s test, therefore there is no ACL tear

Affirming the consequent: If P implies Q, and Q is true, the P is true (INVALID)

Clinical example: If an ACL tear implies a positive Lachman’s test, and the patient has a positive Lachman’s test, that patient has an ACL tear

Denying the antecedent: If P implies Q, and P is false, then Q is false (INVALID)

Clinical example: If an ACL tear implies a positive Lachman’s test, and the patient does not have an ACL tear, that patient will have a negative Lachman’s test

I hope this helps. It will help even more if someone familiar with logic, Bayes, and clinical inquiry guides you through it.

As always, stay curious!